Обучение составлению эвристических алгоритмов, как способ развития творческих способностей младших школьников

Страница 1

В настоящее время нашей стране нужны люди, способные принимать нестандартные решения, умеющие творчески мыслить. Уже давно ученые пытались разгадать загадку творчества и выявили психологические составляющие, необходимые для творческой деятельности. Это:

- гибкость ума, включающая способность к выделению существенных признаков из множества случайных и способность быстро перестраиваться с одной идеи на другую;

- систематичность и последовательность мышления, позволяющая управлять процессами творчества;

- диалектичностъ мышления, при которой мыслящий человек может четко сформулировать противоречие и найти способ его разрешения;

- способность выдвигать гипотезы и уметь их проверять.

Одним из эффективных средств развития творческого мышления являются эвристические задачи. Такие задачи требуют "открыть" (разработать) специфический способ достижения поставленной цели, точно и понятно описать его. Эвристические задачи вовлекают детей в творческую поисковую деятельность, содействуют развитию многих общеинтеллектуальных умений.

Решение эвристических задач требует умения работать с алгоритмами, т.е. планировать последовательность действий для достижения какой-либо цели, а также решать широкий класс задач, для которых ответом является не число или утверждение, а описание последовательности действий.

При творческом подходе к проблеме необходимо выявить новые свойства конкретной ситуации. Особенно важно это при выполнении нестандартных заданий, не имеющих аналогов решения. В таких заданиях сама проблема не всегда четко определена и поэтому нуждается в окончательном формулировании. От решающего требуется умение построить проблемную ситуацию: выделить проблему и критерии оптимального решения.

Задача. Среди трех монет одна фальшивая, она отличается по весу от остальных. Причем неизвестно, легче она или тяжелее. Как с помощью чашечных весов без гирь найти фальшивую монету?

По условию задачи у нас всего три монеты, поэтому положить на чашечку весов можно только по одной монете. Назовем эти монеты "первая" и "вторая" и нарисуем возможные варианты первого взвешивания:

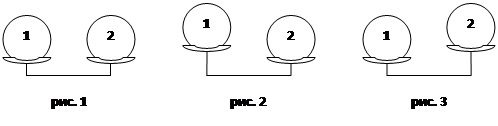
Если весы уравновесились (рис. 1), то первая и вторая монеты одинаковые, т.е. настоящие, значит, фальшивая монета - третья.

Если же весы не уравновесились (рис. 2 и 3), то одна из двух взвешиваемых монет фальшивая, а третья будет точно настоящей, так как фальшивая монета по условию задачи только одна. Чтобы узнать, какая монета из двух фальшивая, надо взвесить одну из "подозреваемых" монет и настоящую. Возможны два варианта выбора монет для взвешивания. Можно взвесить первую монету и третью или вторую и третью. При таких взвешиваниях возможны два результата: весы уравновесятся или нет. Если вес взвешиваемых монет будет равен, значит, фальшивая оставшаяся монета, если нет, то фальшивая - взвешиваемая «подозреваемая» монета.

Ответом этой задачи является разветвляющийся алгоритм. Его можно записать словами, и тогда получится целое сочинение. Такая форма записи очень громоздка и неудобна для анализа. Поэтому в начальных классах можно предложить оформить такой алгоритм в виде блок-схемы. Например:

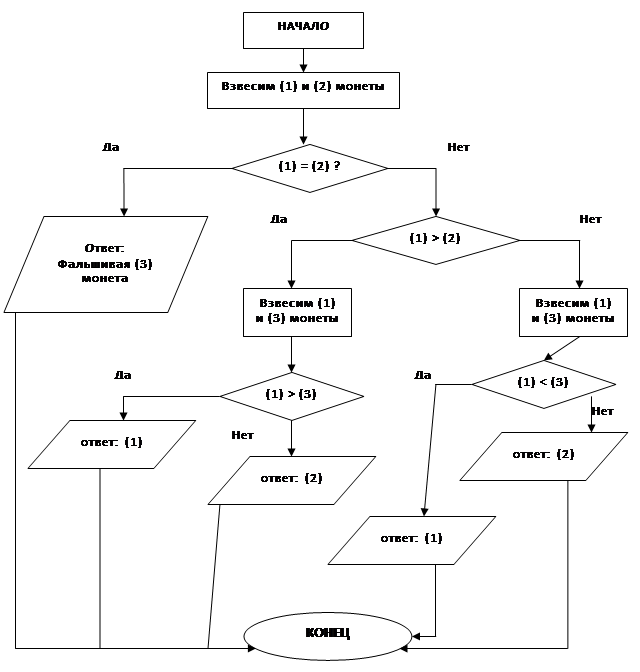
Для обучения составлению блок-схем решения разветвляющихся эвристических задач целесообразно использовать задания по восстановлению блок-схем. При этом ученики анализируют каждый блок схемы, определяют возможные варианты по заполнению пропущенных блоков, что способствует развитию гибкости ума. Эти задания обладают и развивающим эффектом, поскольку деятельность учеников по заполнению готовой блок-схемы основана на таких интеллектуальных умениях, как умение анализировать, обобщать, сравнивать, делать выводы из данных условий.

Задание. Поставьте в блок-схеме второго способа решения предыдущей задачи знаки >, < или = так, чтобы получилось верное решение.

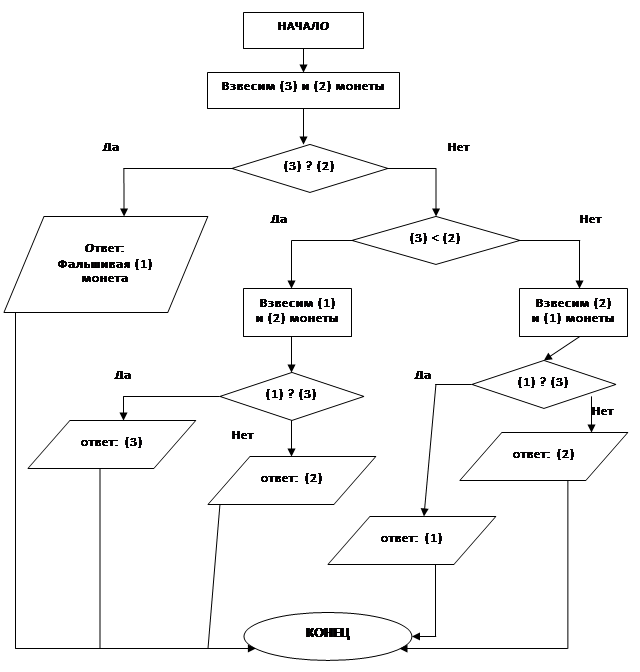
К задачам на составление эвристических алгоритмов относятся задачи на переливание.

Мышление как высшая форма познания. Виды мышления
Мышление - процесс познавательной деятельности индивида, характеризующийся обобщенным и опосредованным отражением действительности. Мышление - это опосредованное - основанное на раскрытии связей, отношений, опосредований - и обобщенное познание объективной реальности. М является высшим познавательным психич процессом. Мышление – это о ...

Источники, движущие силы и закономерности психического развития
Выготский: психическое развитие относится к непреформирующему способу развития, т.е. не определен ни результат, ни стадии. Преформирующий – с самого начала определен и задан конечный результат и стадии. Псих. развитие – особый процесс внутри непроформ. типа, т.к. существует детерминанта, к-я задаёт конечный результат и стадии. Это урове ...

Понятие воображения. Функции и свойства воображения
Воображение – это психический процесс, который заключается в создании новых образов на основе данных прошлого опыта. Человек может мысленно представить себе то, что в прошлом не воспринимал или не совершал, у него могут возникать образы предметов и явлений, с которыми он раньше не встречался. Процесс воображения свойствен только челов ...